Oui, oui, il existe aussi une multitude de blagues sur les maths !
Mais bon, pour l’équilibre psychologique de mes hypothétiques lecteurs, j’ai choisi de ne pas écrire toutes la série des blagues de maths du type « C’est logarithme et exponentielle » qui vont au resto, en soirée…
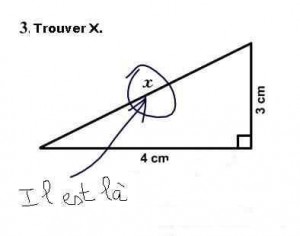
Jésus et les maths :
Jésus, debout sur son rocher, parle à ses disciples et leur dit :
« y²=2px »
Un des apôtres prend alors la parole :
« Écoute, Jésus, déjà d’habitude on comprend pas grand chose à ce que tu nous dis, mais là, franchement on est perdus. »
Mais Jésus leur répond :
« C’était une parabole… »
1+1 n’est sûrement pas égal à 2
Démonstration :
On part d’une égalité de deux réels a et b
a=b
On multiplie les deux membres par a
a²=ab
On soustrait b² aux deux membres
a²-b²=ab-b²
On factorise
(a+b)(a-b)=b(a-b)
On simplifie par (a-b)
a+b=b
On prend a=1 et b=1
1+1=1
(pour ceux qui croiraient cette démo exacte, n’appelez pas l’académie des sciences pour autant…)
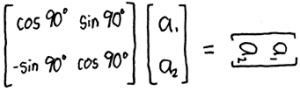
Tout entier naturel est intéressant
Démonstration :
Par l’absurde, supposons qu’il existe au moins un entier naturel non intéressant.
Alors l’ensemble des entiers non-intéressants admet une borne inférieure qui est un minimum car cet ensemble est un ensemble d’entiers non vide et minoré par 0.
Mais, ce minimum est quand même vachement intéressant !
Contradiction.
L’injectivité implique la surjectivité
Démonstration :
Soit f une fonction injective.
Alors tout élément possède au plus un antécédent par f
Or, qui peut le plus peut le moins (c’est bien connu !)
Donc tout élément possède au moins un antécédent par f
Donc f est surjective.
Maths et vie de couple
Un médecin, un avocat et un mathématicien discutent des mérites comparés d’une épouse et d’une maîtresse.
L’avocat :
« Il vaut mieux avoir une maîtresse. En cas de divorce, une épouse pose de nombreux problèmes légaux. »
Le médecin :
« Il vaut mieux avoir une épouse, car le sentiment de sécurité réduit le stress, et c’est bon pour la santé. »
Le mathématicien :
« Vous avez tous les deux tort. Le mieux est d’avoir les deux. Quand votre femme vous croit chez votre maîtresse, et votre maîtresse chez votre femme, vous pouvez faire des maths. »
Plusieurs sortes de gens
Il y a dix sortes de gens : ceux qui savent compter en binaire et ceux qui ne le savent pas.
Il y a deux sortes de gens : ceux qui pensent que le monde peut être divisé en deux sortes de gens et ceux qui pensent que ce n’est pas possible.
Classer les problèmes mathématiques en tant que linéaire et non-linéaire est comme classer les choses de l’Univers en tant que bananes et non-bananes.
Je ne pense pas donc je ne suis pas
Un soir, René Descartes vint se détendre dans une taverne.
Le patron lui demanda : « Bonsoir, Monsieur Descartes, la même chose que d’habitude ? ».
Descartes répondit « Hum … Je ne pense pas » et il se désintégra.
Le rêve de tout étudiant
Un prof et deux étudiants se promènent quand ils trouvent une vieille lampe à huile qui se révèle être une lampe à génie.
Celui-ci leur offre un voeu à chacun.
Le premier étudiant demande à être envoyé à Hawaï avec une superbe hawaiienne nue et follement amoureuse de lui…
Le génie prononce deux-trois formules et l’étudiant disparaît vers un monde de volupté !
Le second lui demande à partir en Suède dans un sauna particulier où il serait le seul homme au milieu de nombreuses suédoises folles de lui.
Le génie prononce trois-quatre formules et l’étudiant disparaît vers un monde de volupté !
Puis il se tourne vers le prof et lui demande son voeu.
Le prof réfléchit un peu et dit : « Je souhaite que tu me ramènes ces deux imbéciles au labo immédiatement… »
Pi
 On demande à plusieurs scientifiques : » Combien vaut pi ? »
On demande à plusieurs scientifiques : » Combien vaut pi ? »
L’ingénieur répond : « C’est approximativement 3 et 1/7. »
Le physicien dit : « C’est 3.14159 »
Le mathématicien réfléchit un instant et répond : « C’est égal à pi ».
Logique
Deux logiciens se rencontrent :
« Salut vieux ! J’ai de bonnes nouvelles ! Ma femme a récemment mis au monde notre premier enfant !
– Félicitations ! C’est un garçon ou une fille ?
– Oui. »
Soustraction
Combien de fois peut-on soustraire 11 de 89 et combien reste-t-il ?
Réponse : autant de fois que l’on veut et il reste 78 à chaque fois.
Limite
La limite quand n tend vers l’infini de sin x /n est 6.
Démonstration :
Il suffit de simplifier par n au numérateur et au dénominateur.
Moutons d’Ecosse
Un mathématicien, un physicien et un ingénieur voyagent à travers l’Ecosse et voient un mouton noir par la fenêtre du train.
« Aha, » dit l’ingénieur, « Je vois que les moutons écossais sont noirs. »
« Hmm, » dit le physicien, « .Tu veux dire que certains moutons écossais sont noirs »
« Non » dit le mathématicien, « Tout ce qu’on sait est qu’il y a au moins un mouton en Ecosse, et qu’au moins un côté de ce mouton est noir ! »
Mathématiques et montgolfières
Deux personnes qui font un tour en montgolfière sont perdues. Elles décident de descendre un peu pour demander leur chemin.
Elles aperçoivent deux hommes qui discutent sur la route. Elles s’approchent et demandent :
« Excusez-moi, mais pouvez vous nous dire ou nous sommes ? »
Les deux hommes se regardent, délibèrent un moment, puis répondent :
« Vous êtes dans une montgolfière ! »
Les deux personnes de la montgolfière, un peu surpris, remercient quand même et reprennent de l’altitude.
Un peu plus loin, l’un dit à l’autre :
« À mon avis, ces deux-là, c’était des mathématiciens.
– Qu’est-ce qui te fait dire ça ?
– Eh bien, ils ont mis beaucoup de temps à nous répondre. Ce qu’ils nous ont dit est parfaitement juste. Et ça ne nous sert absolument à rien. »
Pendant ce temps, les deux mathématiciens disent :
« À mon avis, c’était des physiciens : ils nous posent des question évidentes, et après, s’ils sont perdus, ça va être de notre faute ! »
Tous les objets sont de la même couleur
Démonstration :
Montrons que n objets sont de la même couleur par récurrence sur n
Pour n=1 c’est clair
On suppose la propriété vraie au rang n
Considérons n+1 objets.
Alors, d’après l’hypothèse de récurrence :
– les n premiers objets sont de la même couleur
– les n derniers objets sont de la même couleur
Donc n+1 objets sont de la même couleur
Donc tous les objets sont de la même couleur.
CHEVAL
————- = π
OISEAU
Démonstration :
En effet : CHEVAL = VACHE * L
Une vache est une bête à pis (β * π)
Un oiseau est une bête à ailes (β * L)
CHEVAL VACHE * L β * π * L
———- = ————– = ———– = π
OISEAU OISEAU β * L
En plus, on vient de démontrer que π est irrationnel car un cheval et un oiseau n’ont vraiment aucun point commun.
Extinction d’un feu
On demande à un ingénieur, un physicien et un mathématicien d’éteindre un feu
L’ingénieur prend un seau d’eau et éteint le feu.
Le physicien : après avoir mesuré la hauteur de la flamme, la pression, la température etc…, il calcule la quantité minimale d’eau pour éteindre la flamme.
Le mathématicien : « D’après un théorème célèbre, il existe une solution pour éteindre ce feu ».
Construction de clôtures
On demande à un ingénieur, un physicien et un mathématicien de construire un enclos pour y mettre des moutons.
L’ingénieur regroupe les moutons et construit une clôture autour.
Le physicien construit une palissade en ligne droite qui est en réalité un cercle de diamètre infini.
Le mathématicien construit une petite cloture autour de lui et se définit comme l’extérieur.
Biologie mathématique
Un ours polaire, c’est un ours cartésien qui a changé de repère.
Un peu d’algèbre
Qu’est-ce qui est jaune, normé et complet ?
Réponse : un espace de Bananach
Complétude
Comment fait-on pour savoir si une porcherie est complète ?
Réponse : on prend une suite de cochons
Mathématiques et cuisine
On rappelle la recette de cuisson des pâtes.
– Remplir une casserole d’eau avec un filet d’huile
– Faire bouillir
– Mettre les pâtes
– Remuer
– Faire cuire 7 minutes
– Goûter
– Egoutter
On donne à un mathématicien une casserole d’eau bouillante et on lui demande de faire cuire des pâtes. Comment procède-t-il ?
Réponse : Il vide l’eau et se ramène au cas précédent…
Modélisation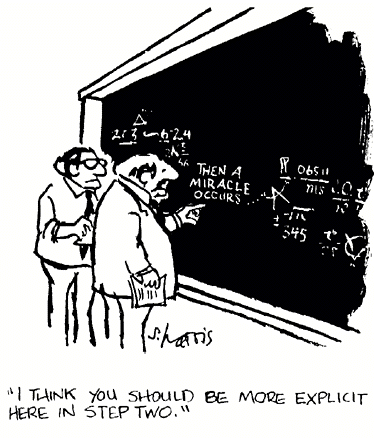
Un homme d’affaires engage un mathématicien, un informaticien et un physicien afin de pouvoir gagner à tous les tiercés.
Le mathématicien le premier s’attaque à la tâche, il calcule des matrices à n’en plus finir, pose des axiomes à tout bout de champ et après de longues semaines de lemmes, théorèmes et conjectures, il conclut que le problème est formellement irrésolvable.
Ensuite, l’informaticien heureux d’avoir vu le mathématicien en échec, s’approche de son Cray III et après avoir écrit quantités d’algorithmes en C++ et introduit tous les paramètres et conditions initiales annonce joyeusement qu’il faudra juste quelques centaines d’années pour calculer le résultat de chaque tiercé…
Le physicien, le sourire aux lèvres, informe ses éminents collègues qu’il a la solution. Il s’approche d’un tableau noir et tout en dessinant une sphère commence par dire : « Approximons le cheval par une sphère parfaite… »
Incendie
Un prêtre, un physicien, un ingénieur en mécanique et un mathématicien sont au dernier étage d’un immeuble en feu. Le seul moyen de s’en sortir et de sauter par la fenêtre dans une piscine située sur le toit de l’immeuble d’en face, un peu moins haut, mais le saut semble difficile.
Le prêtre se place à la fenêtre, prie, saute. Il atterrit de justesse dans la piscine, à quelques cm du bord.
Le physicien mesure la vitesse du vent, la distance, la différence de hauteur et trouve un charbon avec lequel il fait un calcul de trajectoire sur le mur pour déterminer la vitesse et l’angle initial nécessaire pour atterrir au milieu de la piscine. Quand il termine, les flammes commencent déjà à se rapprocher dangereusement de leur étage. Il prend son élan, saute, et atterrit de justesse dans la piscine, à quelques cm du bord.
L’ingénieur ramasse une planche, mesure son élasticité, l’accroche sur le bord de la fenêtre, et utilise les données du physicien pour faire des calculs. Il couvre un mur entier, le sol commence à chauffer à cause de la proximité des flammes. Finalement, il termine son calcul, va sur la planche, saute, et atterrit dans la piscine, à peine moins loin du bord que le physicien.
Le mathématicien a maintenant à sa disposition les données du physicien et de l’ingénieur. Il commence ses calculs, couvre un mur, deux murs, les flammes commencent à entrer par la porte, et il n’y a finalement plus un seul mur de libre quand il a terminé. Il se met sur la planche, saute, et part tout droit en l’air. On ne le voit plus retomber. Que s’est-t’il passé?
Une erreur de signe.

